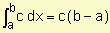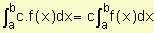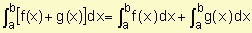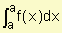Justificación

El avance de la ciencia y la tecnología nos indica que diferentes fenómenos de la naturaleza se explican mediante modelos matemáticos. Para llegar a formular dichos modelos se requiere que el estudiante tenga conocimientos precisos y amplios de Matemáticas.

El Cálculo es una herramienta poderosa para analizar el mundo real. Los estudiantes adquieren una comprensión del poder del Cálculo cuando se enfocan hacia sus aplicaciones en un problema extenso. El Cálculo Integral es un curso que prepara los estudiantes de ingeniería para abordar cursos de Matemáticas más avanzados donde se necesita su aplicación

El curso está orientado a la enseñanza de las aplicaciones y utilización de las Matemáticas para mejorar en los estudiantes sus habilidades en el uso de diversas técnicas (Derive, Maple, Matlab).

Resalta sobre todo lo anterior, la necesidad de un manejo adecuado del cálculo integral, el cual nos permite determinar: áreas bajo una curva y volúmenes, siendo de gran aplicación en la ingeniería y contribuyendo a la capacidad de análisis del estudiante, aportándole elementos técnicos que le permitan la solución de problemas físicos inherentes a la carrera, así como a los de la especialidad en general.

Para ver la carta descriptiva del curso, hacer clic acá.


.

Herramientas Digitales para el Curso

En la carta descriptiva se mencionan los textos que servirán como guía para el curso. Comparto con ustedes uno de los textos en formato PDF para consulta de ejercicios, ejemplos, etc:

• Calculo de  Leithold-7a.Ed.

Y para corroborar los resultados obtenidos, recomiendo el software Derive, que es una potente herramienta, facil de usar:

• Características de Derive. 

UNIDAD 1: Integral Indefinida Parte 1

La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.

Por ejemplo,nos piden hallar una función F, cuya derivada sea f(x)= 3x²

Probablemente diríamos que:

F(x)= x³ ya que d/dx[x³]= 3x²

Decimos que F es una antiderivada de f y no que es la antiderivada de f. la razón es que, por ejemplo:

Son todas ellas antiderivadas de f(x)= 3x²

En General para cualquier valor de la constante C, F(x)= x³es antiderivada de f(x).

Reglas básicas de integración

• Reglas básicas de integración (haciendo clic acá) 

 Ejemplos:

 

TALLER 1: 

• Antiderivadas e integración indefinida

 Métodos de Integración

Integración por sustitución:

El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.

∫ƒ'(g(x))g'(x)dx = ∫ƒ(u)du = F(u)+C = F(g(x))+C

Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable u, de modo que se obtenga una integral más sencilla.

Observese la página 5 del siguiente documento dando clic acá 

TALLER 2:

• Integración indefinida por sustitución 

Integración por partes:

Supóngase que u = f(x) y v = g(x) son funciones diferenciables. Por la regla de la derivada del producto de dos funciones se tiene que:

^{d/_{dx  [f(x)g(x)] = f(x)g'(x)+f '(x)g(x)}}

^{_{Si integramos a ambos lados de la igualdad obtenemos:}}

∫^{d/_{dx [f(x)g(x)] dx = ∫[f(x)g'(x)] dx + ∫[f '(x)g(x)]dx}}

   ∫[f(x)g'(x)] dx =  f(x)g(x) - ∫[f '(x)g(x)]dx

Haciendo a u = f(x) y v = g(x) y sus derivadas du = f ' (x)dx y dv = g'(x)dx.

Tenemos: 

∫udv = uv - ∫vdu 

Nosotros debemos escoger adecuadamente u que sea facil de derivar y dv que sea facil de integrar.

¿cómo sabemos si una elección está bien? Para saber ello tenemos el concepto LIATE, que es la forma reducida para considerar los casos de funciones que podemos tener para “u” y el orden de jerarquías: 

 L: Logaritmos; 

 I: Inversas; 

A: Algebraicas; 

T: Trigonométricas; 

E: Exponencial. 

Como vemos entonces, el secreto está siempre en escoger “u” basado en este sistema de jerarquías.

Para mas ejemplos visitar LIATE en la integración por partes.


TALLER 3:

•  Integración por partes 

Producto de potencias de seno y coseno

   
       Potencias enteras positivas para tanx:

tomado de: http://www.calculointegrales.com/p/integrales-trigonometricas.html

Para ampliar la información ir a http://www.fic.umich.mx/~lcastro/capitulo7.pdf


TALLER 4:

• Integrales trigonométricas

PARCIAL 1 (haciendo clic acá)

UNIDAD 2 Integral indefinida Parte 2

Integración por sustitución trigonométrica

Podemos usar el método de sustitución trigonometrica para resolver integrales en que aparezcan lo radicales, √(a²-u²), √(a²+u²), √(u²-a²).
El objetivo consiste en eliminar los radicales del integrando. Con este fin, usamos las identidades pitagóricas:

• cos²θ = 1-sen²θ

• sec²θ = 1+tan²θ

• tan²θ = sec²θ-1 

Pasos:

1. Para integrales que contienen √(a²-u²), sea u=asenθ, entonces: √(a²-u²) = acosθ.
2. Para integrales que contienen √(a²+u²), sea u=atanθ, entonces: √(a²+u²) = asecθ.
3. Para integrales que contienen √(u² -a²), sea u=asecθ, entonces: √(a²-u²) = atanθ.

TALLER 1:

• Integración por sustitución trigonométrica

Integración Fracciones simples

Consiste en descomponer funciones racionales en otras funciones racionales más simples a las que se le puede aplicar las formulas básicas de integración.

    la cuestión es ¿cómo determinar las fracciones simples para representar el primer integrando?
Sabemos combinar funciones tales como:

El método de las fracciones simples enseña como invertir el proceso:

Método y Ejemplos para expresar una fracción en sus fracciones simples haciendo clic acá

TALLER 2:

• Integración por fracciones parciales

Integración usando tabla

Cuando alguna integral no puede ser resuelta por los métodos vistos anteriormente, lo mejor es acudir a la tabla de integrales y buscar la forma general que se "acomode" a la integral que debemos resolver. 

La tabla de integrales está dividida en:

• Formas que contienen  
• Formas que contienen  
• Formas que contienen con  
• Formas que contienen  
• Formas que contienen  
• Formas que contienen sen u, cos u, tan u, cot u, sec u y csc u.
• Formas que contienen y     

 Descarga la tabla dando clic acá

TALLER 3: 

• Integración usando tablas 

 

PARCIAL 2 (Haciendo clic acá) 

UNIDAD 3: Regla de L’hopital e Integral Definida

Regla de L'hopital:

El método general para calcular el límite en un número a de una función que tiene la forma indeterminada 0/0 en a emplea un teorema conocido como La regla de L´hopital en honor al matemático francés Guillaume Francois de L´hopital (1661-1707).

Regla de L´hopital: 
Sean f y g dos funciones diferenciables en un intervalo abierto I, excepto posiblemente en un número a de I, supongase que para todo x de I, ,  y que  . Si y  y si

entonces   

Ejemplos de Regla de L´hopital dando clic acá 

TALLER 1:

• ejercicios de regla de L'hopital

Integral Definida: 
 Determinar el área de figuras planas no es ningún problema, siempre y cuando estas tengas figuras conocidas a las cuales podemos seccionar, hallar las áreas y sumar.

 Pero al momento de determinar áreas de curvas la situación no es tan elemental.
Determinar áreas bajo curvas o áreas entre curvas es uno de las tantas aplicaciones que tienen las integrales en situaciones de la vida real.

SUMATORIA

Definición de la notación sigma:

 Donde m y n son números enteros y m<n. m se denomina límite inferior y n límite superior.

TALLER 2:

• Sumatoria

ÁREA

PROPIEDADES Y TEOREMAS DE LA INTEGRAL DEFINIDA

Propiedades Teoremas

Cálculo de áreas entre dos curvas

Ver Ejemplo

PROPIEDADES DE LA INTEGRAL DEFINIDA

Se enuncian algunas propiedades y teoremas básicos de las integrales definidas que ayudarán a evaluarlas con más facilidad. 
1)

  donde c es una constante

2) Si f y g son integrables en [a, b] y c es una constante, entonces las siguientes propiedades son verdaderas:

(se pueden generalizar para más de dos funciones)

3) Si x está definida para x = a entonces   

= 0

4) Si f es integrable en [a, b] entonces   

Ejemplos de integral definida

 

TALLER 3:

• Integral definida

Área bajo la curva

III-3. Integral Definida - Área entre Curvas from Ugma

TALLER 4:

• Área bajo la curva y entre curvas 

PARCIAL 3 

UNIDAD 4: Solidos de Revolución, aplicaciones.

Solidos de Revolucion by Jhon Darwin Erazo

TALLER 1

• Sólidos de revolución

Longitud de arco
La longitud del arco, de la curva f(x), comprendido entre las abscisas x = a y x = b viene dado por la integral definida:

Ejemplo

Hallar la longitud del arco de curva función en el intervalo [0, 1].

 

Que es aproximadamente 1.44 um.

TALLER 2:

• Longitud de Arco